Abstract

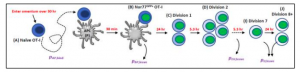
The Stochastic Omentum REsponse (STORE) model is a mathematical system that describes how T-cells in the omentum (a fatty-tissue in the body that is a key part of the immune system) respond when encountering antigens arising from either infection or vaccination of various kinds. In the omentum, T-cells that encounter antigen presenting cells (APCs) go through various stages of priming and cell division before leaving the omentum in pursuit of the foreign body (such as a virus) so that it can be destroyed.

The STORE model accepts user parameters as input such as the amount of certain types of cell present in the omentum and/or how quickly they enter the omentum, parameters that describe how likely T-cells will interact with APCs, and parameters that describe probabilities of T-cells leaving the omentum at various stages of cell division. Each individual cell is tracked within the model using an efficient strategy, with cell counts that can reach millions during the expansion phase of an immune system response. The output of the model is a data table of the cell counts of each type and how they change throughout the system response over time.

Applications

• Modeling in immunology, virology, and pathology.
• Rapidly create vaccines of all types, including COVID-19
• Determine best dosages and vaccination schedules to use during the first human trials or later stage trials
• Determine probability distributions of protective immunity that can be achieved and extent of protection

Advantages

• First stochastic,dynamic model of the immune system responses to vaccine injection
• Can be used for live-virus vaccines, attenuated-virus vaccines, vaccine adjuvants, and even simple infection
• Model aspects of the immune system that cannot be measured by experiment; the model fills in the gaps by tracking cells that cannot be or measured through experiment